การคูณ
จากวิกิพีเดีย สารานุกรมเสรี
- "คูณ" เปลี่ยนทางมาที่นี่ บทความนี้เกี่ยวกับคณิตศาสตร์ สำหรับพระสงฆ์ ดูที่ พระเทพวิทยาคม (คูณ ปริสุทโธ)
การคูณสามารถนิยามบนจำนวนธรรมชาติว่าเป็นการบวกที่ซ้ำๆ กัน ตัวอย่างเช่น 4 คูณด้วย 3 (หรือเรียกโดยย่อว่า 4 คูณ 3) หมายถึงการบวกจำนวน 4 เข้าไป 3 ชุด ดังนี้
การคูณอาจมองได้จากการนับวัตถุที่จัดเรียงกันเป็นรูปสี่เหลี่ยมผืนผ้า (สำหรับจำนวนธรรมชาติ) หรือการหาพื้นที่ของรูปสี่เหลี่ยมผืนผ้าโดยการหนดความยาวของด้านมาให้ (สำหรับจำนวนทั่วไป) ส่วนกลับของการคูณคือการหาร ในเมื่อ 4 คูณด้วย 3 เท่ากับ 12 ดังนั้น 12 หารด้วย 3 ก็จะเท่ากับ 4 เป็นต้น
การคูณสามารถนิยามให้ขยายไปบนจำนวนชนิดอื่นเช่นจำนวนเชิงซ้อน และมีโครงสร้างที่เป็นนามธรรมมากขึ้นเช่นเมทริกซ์
เนื้อหา[แสดง] |
[แก้] สัญกรณ์และคำศัพท์เฉพาะทาง

เครื่องหมายคูณ ลักษณะคล้ายกากบาท
-
 (อ่านว่า 2 คูณ 3 เท่ากับ 6)
(อ่านว่า 2 คูณ 3 เท่ากับ 6)


- ใช้จุดกลาง (·) หรือไม่ก็มหัพภาค (.) อย่างใดอย่างหนึ่ง เช่น 5 · 2 หรือ 5 . 2 การใช้จุดกลางเป็นมาตรฐานในสหรัฐอเมริกา สหราชอาณาจักร และประเทศอื่นๆ ที่ใช้มหัพภาคเป็นจุดทศนิยม แต่ในบางประเทศที่ใช้จุลภาคเป็นจุดทศนิยม จะใช้มหัพภาคเป็นการคูณแทน
- ใช้ดอกจัน (*) เช่น
5*2มักใช้ในภาษาโปรแกรมเพราะเครื่องหมายนี้ปรากฏอยู่บนทุกแป้นพิมพ์ และสามารถดูได้ง่ายบนจอมอนิเตอร์รุ่นเก่า การใช้เครื่องหมายนี้แทนการคูณเริ่มมีขึ้นตั้งแต่ภาษาฟอร์แทรน - ในพีชคณิต การคูณที่เกี่ยวกับตัวแปรมักจะเขียนให้อยู่ติดกัน เรียกว่า juxtaposition ตัวอย่างเช่น xy หมายถึง x คูณ y และ 5x หมายถึง 5 คูณ x เป็นต้น สัญกรณ์เช่นนี้สามารถใช้กับจำนวนที่ครอบด้วยวงเล็บ เช่น 5(2) หรือ (5)(2) ก็จะหมายถึง 5 คูณ 2
- ในการคูณเมทริกซ์ มีความแตกต่างระหว่างการใช้สัญลักษณ์กากบาทกับจุด กากบาทใช้แทนการคูณเวกเตอร์ ในขณะที่จุดใช้แทนการคูณสเกลาร์ ดังนั้นการตั้งชื่อเรียกจึงแตกต่างกันคือผลคูณไขว้และผลคูณจุดตามลำดับ
ผลลัพธ์ที่เกิดจากการคูณเรียกว่า ผลคูณ (product) หรือเรียกว่า พหุคูณ (multiple) ของตัวประกอบแต่ละตัวที่เป็นจำนวนเต็ม ตัวอย่างเช่น 15 คือผลคูณของ 3 กับ 5 และในขณะเดียวกัน 15 ก็เป็นทั้งพหุคูณของ 3 และพหุคูณของ 5 ด้วย
[แก้] ผลคูณของลำดับ
ถ้าพจน์แต่ละพจน์ของผลคูณไม่ได้เขียนออกมาทั้งหมด เราอาจจะใช้เครื่องหมายจุดไข่ปลาแทนพจน์ที่หายไป เช่นเดียวกับการดำเนินการอื่นๆ (เช่น การบวก) เช่น ผลคูณของจำนวนธรรมชาติ ตั้งแต่ 1-100 อาจเขียน . และสามารถเขียนให้เครื่องหมายจุดไข่ปลาอยู่บริเวณกึ่งกลางแนวตั้งของแถวได้อีกด้วย คือ
. และสามารถเขียนให้เครื่องหมายจุดไข่ปลาอยู่บริเวณกึ่งกลางแนวตั้งของแถวได้อีกด้วย คือ  .
.นอกจากนี้แล้ว ผลคูณยังสามารถเขียนได้ด้วยเครื่องหมายผลคูณ ซึ่งมาจาก อักษร Π (Pi) ตัวใหญ่ ในอักษรกรีก. ตัวอย่างเช่น
[แก้] นิยาม
สำหรับความหมายของการคูณ ผลคูณของจำนวนธรรมชาติ n และ m ใดๆ- m × n = m + m + m + ... + m
- 5 × 2 = 2 + 2 + 2 + 2 + 2 = 10
- 2 × 5 = 5 + 5 = 10
- 4 × 3 = 3 + 3 + 3 + 3 = 12
- m × 6 = m + m + m + m + m + m
- x · y = y · x.
- (x · y)z = x(y · z).
การคูณมีสมบัติการแจกแจง เพราะ
- x(y + z) = xy + xz.
- 1 · x = x.
สำหรับเลข 0 เราจะได้
- m · 0 = m + m + m +...+ m
- m · 0 = 0
การคูณกับจำนวนลบอาจจะต้องมีการคิดเล็กน้อย เริ่มจากการคูณ (−1) กับจำนวนเต็ม m ใดๆ
- (−1)m = (−1) + (−1) +...+ (−1) = −m
- (−1)(−1) = −(−1) = 1
หลายคนอาจสงสัยถ้าบอกว่า ผลคูณของ'ไร้จำนวน' คือ 1
รูปแบบนิยามเรียกซ้ำของการคูณเป็นไปตามกฎ
- x · 0 = 0
- x · y = x + x·(y − 1)
[แก้] การคำนวณ
วิธีการคูณจำนวนโดยการทดลงกระดาษตามปกติ จำเป็นต้องใช้สูตรคูณที่ท่องจำ ซึ่งเป็นผลคูณของเลข 1−2 หลัก เพื่อให้สามารถตั้งคูณได้ แต่สำหรับวิธีการแบบชาวอียิปต์โบราณไม่เป็นเช่นนั้น ดังที่จะได้กล่าวต่อไปการคูณจำนวนมากกว่าสองจำนวนบนเลขฐานสิบอาจทำให้เกิดความเบื่อหน่าย และก่อให้เกิดความผิดพลาดได้ง่าย จึงมีการคิดค้นลอการิทึมสามัญ (ลอการิทึมฐานสิบ) เพื่อทำให้คำนวณง่ายขึ้น นอกจากนั้นสไลด์รูลก็เป็นเครื่องมือช่วยคูณจำนวนอย่างรวดเร็ว และได้ผลลัพธ์ที่มีความแม่นยำประมาณสามหลัก และตั้งแต่ต้นคริสต์ศตวรรษที่ 20 ก็มีการประดิษฐ์เครื่องคิดเลขเชิงกล ซึ่งสามารถคูณเลขได้โดยอัตโนมัติถึง 10 หลัก ปัจจุบันนี้ใช้เครื่องคิดเลขอิเล็กทรอนิกส์และคอมพิวเตอร์แทน ซึ่งสามารถช่วยประหยัดเวลาการคูณเลขไปได้อย่างมาก
[แก้] ขั้นตอนวิธีในประวัติศาสตร์
วิธีการคูณหลายวิธีมีการบันทึกไว้เป็นลายลักษณ์อักษรโดยอารยธรรมอียิปต์ กรีซ บาบิโลเนีย ลุ่มแม่น้ำสินธุ และจีน[แก้] อียิปต์
- ดูบทความหลักที่ การคูณแบบอียิปต์โบราณ
13 × 21 = (1 + 4 + 8) × 21 = (1 × 21) + (4 × 21) + (8 × 21) = 21 + 84 + 168 = 273
[แก้] บาลิโลเนีย
เนื่องจากชาวบาบิโลนใช้ระบบเลขประจำหลักฐานหกสิบ ซึ่งเทียบได้กับเลขฐานสิบของปัจจุบัน แต่มีสัญลักษณ์แทนเลขโดดในแต่ละหลักถึง 60 ตัว ดังนั้นการคูณของชาวบาบิโลนจึงคล้ายกับวิธีการตั้งคูณในปัจจุบัน แต่เนื่องจากเป็นการยากที่จะจดจำผลคูณที่แตกต่างกันทั้งหมด 60 × 60 จำนวน นักคณิตศาสตร์ชาวบาบิโลนจึงใช้ตารางการคูณ (สูตรคูณ) เข้าช่วย ตารางเหล่านี้ประกอบด้วยรายชื่อของพหุคูณ 20 จำนวนแรกของจำนวนที่สำคัญ n ซึ่งจะได้ n, 2n, ..., 20n ตามด้วยพหุคูณของ 10n นั่นคือ 30n, 40n, และ 50n การคำนวณผลคูณคือการบวกค่าในตารางผลคูณเข้าด้วยกัน เช่น 53n ก็หาได้จากการบวกค่าของ 50n กับ 3n เป็นต้น[แก้] จีน
ในตำราเรียนคณิตศาสตร์ของจีนชื่อว่า Zhou Pei Suan Ching (周髀算經) เมื่อ 300 ปีก่อนคริสตกาล และหนังสือ The Nine Chapters on the Mathematical Art (九章算術) ได้อธิบายวิธีการคูณโดยการเขียนเป็นตัวหนังสือ ถึงแม้ว่านักคณิตศาสตร์ชาวจีนสมัยก่อนจะใช้ลูกคิดคำนวณด้วยมือทั้งการบวกและการคูณ[แก้] ลุ่มแม่น้ำสินธุ
นักคณิตศาสตร์ชาวฮินดูในอารยธรรมลุ่มแม่น้ำสินธุในสมัยก่อน ใช้กลวิธีที่หลากหลายเพื่อคำนวณการคูณ ซึ่งการคำนวณส่วนใหญ่จะทำบนกระดานชนวนขนาดเล็ก เทคนิคหนึ่งที่ใช้กันคือการคูณแลตทิซ (lattice multiplication) เริ่มตั้งแต่การวาดตารางขึ้นมาหนึ่งตาราง กำกับด้วยตัวตั้งและตัวคูณลงบนแถวและหลัก แต่ละช่องจะถูกแบ่งออกเป็นสองส่วนตามแนวทะแยง เป็นแลตทิซรูปสามเหลี่ยม ซึ่งเฉียงเป็นแนวเดียวกันทุกช่อง จากนั้นแต่ละช่องสี่เหลี่ยมให้เขียนผลคูณของเลขโดดที่กำกับไว้ลงไป ผลคูณของจำนวนจะหาได้จากการรวมแถวที่เป็นแนวเฉียงเข้าด้วยกันทีละหลัก
ที่มาจาก http://th.wikipedia.org/wiki/%E0%B8%81%E0%B8%B2%E0%B8%A3%E0%B8%84%E0%B8%B9%E0%B8%93








 ) แต่นิพจน์
) แต่นิพจน์  ไม่ใช่พหุนาม เนื่องจากมีการหาร เช่นเดียวกับ นิพจน์
ไม่ใช่พหุนาม เนื่องจากมีการหาร เช่นเดียวกับ นิพจน์ 
 อ่านว่า เศษสามส่วนสี่ หรือ สามในสี่ หมายความว่า วัตถุสามชิ้นส่วนจากวัตถุทั้งหมดที่แบ่งออกเป็นสี่ส่วนเท่าๆ กัน นอกจากนั้น การแบ่งวัตถุสิ่งหนึ่งออกเป็นศูนย์ส่วนเท่า ๆ กันนั้นเป็นไปไม่ได้ ดังนั้น
อ่านว่า เศษสามส่วนสี่ หรือ สามในสี่ หมายความว่า วัตถุสามชิ้นส่วนจากวัตถุทั้งหมดที่แบ่งออกเป็นสี่ส่วนเท่าๆ กัน นอกจากนั้น การแบ่งวัตถุสิ่งหนึ่งออกเป็นศูนย์ส่วนเท่า ๆ กันนั้นเป็นไปไม่ได้ ดังนั้น  ,
, 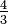 เป็นต้น สำหรับเศษส่วนที่ตัวเศษหรือตัวส่วนไม่เป็นจำนวนเต็ม อาจไม่เป็นจำนวนตรรกยะ นอกจากนั้นเศษส่วนสามัญยังแยกออกเป็นเศษส่วนแท้ (proper fraction) ซึ่งมีค่าของตัวเศษน้อยกว่าตัวส่วน ทำให้ปริมาณของเศษส่วนน้อยกว่า 1 เช่น
เป็นต้น สำหรับเศษส่วนที่ตัวเศษหรือตัวส่วนไม่เป็นจำนวนเต็ม อาจไม่เป็นจำนวนตรรกยะ นอกจากนั้นเศษส่วนสามัญยังแยกออกเป็นเศษส่วนแท้ (proper fraction) ซึ่งมีค่าของตัวเศษน้อยกว่าตัวส่วน ทำให้ปริมาณของเศษส่วนน้อยกว่า 1 เช่น  และเศษเกิน (improper fraction) คือเศษส่วนที่ค่าของตัวเศษมากกว่าหรือเท่ากับตัวส่วน เช่น
และเศษเกิน (improper fraction) คือเศษส่วนที่ค่าของตัวเศษมากกว่าหรือเท่ากับตัวส่วน เช่น  ,
, 
 )
)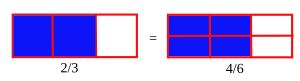
 เทียบเท่ากับ
เทียบเท่ากับ 
 ที่มีค่าเท่ากับ 1 ดังนั้นปริมาณของเศษส่วนจึงไม่เปลี่ยนแปลง ตัวอย่างเช่น กำหนดเศษส่วน
ที่มีค่าเท่ากับ 1 ดังนั้นปริมาณของเศษส่วนจึงไม่เปลี่ยนแปลง ตัวอย่างเช่น กำหนดเศษส่วน  เมื่อคูณด้วย 2 ทั้งตัวเศษและตัวส่วนจะได้ผลลัพธ์เป็น
เมื่อคูณด้วย 2 ทั้งตัวเศษและตัวส่วนจะได้ผลลัพธ์เป็น  ซึ่งยังคงมีปริมาณเท่ากับ
ซึ่งยังคงมีปริมาณเท่ากับ 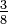 เป็นเศษส่วนอย่างต่ำเพราะมีตัวประกอบร่วมเพียงตัวเดียวคือ 1 ในทางตรงข้าม
เป็นเศษส่วนอย่างต่ำเพราะมีตัวประกอบร่วมเพียงตัวเดียวคือ 1 ในทางตรงข้าม 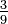 ไม่เป็นเศษส่วนอย่างต่ำเนื่องจากยังสามารถหารด้วย 3 ได้อีกเป็น
ไม่เป็นเศษส่วนอย่างต่ำเนื่องจากยังสามารถหารด้วย 3 ได้อีกเป็น  ตัวส่วนสำหรับการเปรียบเทียบคือ ครน. ของ 4 กับ 18 มีค่าเท่ากับ 36 ดังนั้นจะได้เศษส่วนที่เทียบเท่าได้แก่
ตัวส่วนสำหรับการเปรียบเทียบคือ ครน. ของ 4 กับ 18 มีค่าเท่ากับ 36 ดังนั้นจะได้เศษส่วนที่เทียบเท่าได้แก่  กับ
กับ  ตามลำดับ ทำให้ทราบได้ว่า
ตามลำดับ ทำให้ทราบได้ว่า  เป็นเศษส่วนซ้อน ในการลดรูปเศษส่วนซ้อนสามารถทำได้โดยการหารตัวเศษด้วยตัวส่วน เหมือนการหารธรรมดา ดังนั้น
เป็นเศษส่วนซ้อน ในการลดรูปเศษส่วนซ้อนสามารถทำได้โดยการหารตัวเศษด้วยตัวส่วน เหมือนการหารธรรมดา ดังนั้น  นอกจากนั้นตัวเศษหรือตัวส่วนสามารถเป็นนิพจน์ของเศษส่วนอื่นต่อๆ กันไปได้ อย่างเช่น
นอกจากนั้นตัวเศษหรือตัวส่วนสามารถเป็นนิพจน์ของเศษส่วนอื่นต่อๆ กันไปได้ อย่างเช่น คือ
คือ  และเนื่องจากจำนวนใดๆ หารด้วย 1 จะได้จำนวนเดิม ดังนั้นจำนวนใดๆ จึงสามารถเขียนให้อยู่ในรูปเศษส่วนโดยมีตัวส่วนเท่ากับ 1 ตัวอย่างเช่น 17 เขียนให้เป็นเศษส่วนได้เป็น
และเนื่องจากจำนวนใดๆ หารด้วย 1 จะได้จำนวนเดิม ดังนั้นจำนวนใดๆ จึงสามารถเขียนให้อยู่ในรูปเศษส่วนโดยมีตัวส่วนเท่ากับ 1 ตัวอย่างเช่น 17 เขียนให้เป็นเศษส่วนได้เป็น 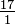 ตัวเลข 1 นี้คือตัวส่วนที่ไม่ปรากฏ ดังนั้นจึงสามารถบอกได้ว่าเศษส่วนและจำนวนทุกจำนวน (ยกเว้น 0) สามารถมีส่วนกลับได้เสมอ จากตัวอย่าง ส่วนกลับของ 17 คือ
ตัวเลข 1 นี้คือตัวส่วนที่ไม่ปรากฏ ดังนั้นจึงสามารถบอกได้ว่าเศษส่วนและจำนวนทุกจำนวน (ยกเว้น 0) สามารถมีส่วนกลับได้เสมอ จากตัวอย่าง ส่วนกลับของ 17 คือ 
 เพราะ
เพราะ  กับ
กับ 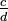 ให้แปลงทั้งสองเป็น
ให้แปลงทั้งสองเป็น  และ
และ  เมื่อได้ว่า
เมื่อได้ว่า  ซึ่งสามารถเปรียบเทียบกันได้
ซึ่งสามารถเปรียบเทียบกันได้



